DESCRIPTION OF THE GURULE SYSTEM OF ORDER

In the 1960’s, paper sculptor Ben Gurule, fell through a trap door from the world of art into the complex wonderland of quantum physics. Through his artistic experiments he inadvertently discovered (and later patented) a previously unknown system of geometric order that just may, oddly enough, cast a new light onto the field of quantum mechanics. His system suggests and illustrates, via a family of 3d models (interdependent matrices), how matter may be produced solely from interlocking circular waves of identical frequency, amplitude, waveform and specific angular phase alignment. These “space cage” structures illustrate how the basic deBroglie matter waves can interweave in such a way as to create complex polyhedral forms (including all the platonic solids) whose shapes and general behavior exhibit striking similarities to some of what quantum physicists have long observed. Each of the waves making up these forms can be viewed as constantly moving. They are networks of occurrence. Hence these structures are dynamic, more like “verbs”. Conventional polyhedra are static, more like “nouns.”

The Gurule System has elements of what a Unified Field Theory would require. His system has baked into it a set of laws that determine how a stable structure, if woven from circular waves, must be constructed. These laws are analogous to much of what is already known about subatomic particle and wave behavior, yet point to the possibility of a new matrix of understanding, a viable Euclidean one nonetheless, that could provide a new framework within which to re-approach some of the ongoing mysteries of quantum mechanics. Topics such as the proton spin crisis, asymptotic freedom (no free quarks), “confinement” in quantum chromodynamics, chirality in particle spin, quantum numbers, type II String Theory (closed strings), and quantum entanglement all come into play. Even the nuclear shell model, electron orbitals, and integer spin take on a completely new meaning when viewed within the fresh context of the Gurule system.

The totality of his patented discovery is mathematically representable though nobody has actually done the math yet. That was beyond Ben’s skill set and could likely involve some combination of Algebraic topology, tensor geometry, braid theory and discrete combinatorial mathematics. The units that make up his system can be thought of as rings (circular pathways, matter waves) which he labels with the letter Q. His system consists of Q1 thru Q7 (1 to 7 rings).

He describes the rings as orbits, whose complete 360 degree loop implies an integer spin of 1, hence the rings can be said to have a “bosonic” nature. These interlocking rings do not touch or interact directly and thus follow Bose-Einstein statistics. (https://en.wikipedia.org/wiki/Bose%E2%80%93Einstein_statistics ) However when another similar structure bumps into it, there will be a limited range of angular interactions that can result in either a bonding or a temporary disfiguring of the base shape. That is, when one of these structures exists in isolation it will have minimum surface tension and hence relax into a sphere. But when in a crowded space with others they get bumped into polyhedral shapes, the specific angles predetermined (with no human intervention) by the physical range of movement inherent to the angle of the wave crossings by which each loop is confined by the others. Hence what results is a lot of triangular, square, pentagonal and hexagonal faces, that are actually spinning vortexes…with either a left or right handed spin. These vortexes are “fermionic” in nature in that several identical ones exist on the surface of the shell but cannot and do not occupy the same quantum state. Some are anti symmetrical but all follow the Pauli Exclusion principle (https://en.wikipedia.org/wiki/Pauli_exclusion_principle) and are made up of components that have partial “spin”. (http://hyperphysics.phy-astr.gsu.edu/hbase/Particles/spinc.html)

Once one of these polyhedral shapes is established it can and will bond with neighboring structures of the same shape, size, wavelength and chirality if touched at the allowable angles for interpenetration. If the rings are spinning in the proper direction neighboring structures will bind together like a nut and a bolt The Gurule system also represents a logical explanation of subatomic AND molecular chirality.
The progression of a structure from Q1 to Q7 etc can occur in two ways, one is volume constant (particle like) and the other is wavelength constant (wavelike).

With “particle-like” expansion (top to bottom in the above picture) of the shell (say Q2 to Q3) all that is needed is the increase of the component wave frequency, hence shortening the wavelength,…in this case by a 2/3 ratio such that in the same spherical volume will now contain 3 waves with 3 wavelengths instead of 2 waves with 2 wavelengths (volume constant). With “wavelike” expansion however, (left to right in above picture) we would add an additional ring and one additional wavelength of the same frequency (to all rings) which would expand the volume of the shell by the distance of one wavelength (wavelength constant). Another interesting property of the system is the “polyhedral shift”, (in math known as “dimension reversing dualities” https://en.wikipedia.org/wiki/Duality_(mathematics)#Dimension-reversing_dualities) which illustrates how by gradually changing the wave shape, amplitude and phase the resulting polyhedron morphs systematically from one platonic solid to its “dual pair” (e.g. cube into octahedron).

Below are a list of further properties and descriptors of the Gurule system:
1. 3d woven models that suggest a new way to look at subatomic particles and their antiparticles

2. The models might be considered to possess “global symmetry”, both continuous and discrete.
(https://core.ac.uk/download/pdf/25243168.pdf)

3. An interdependent 3d matrix that mathematically unites “Euler’s Characteristic” with the nuclear shell model and the electron shells.

a. the number of 2 way crossings match exactly with the number of maximum proton states in the Deformed Harmonic Oscillator Model and their spin orbit interaction. (https://en.wikipedia.org/wiki/Nuclear_shell_model)

b. The maximum number of electrons in each shell (K,L,M,N,O,P,Q)) is equal to, in the Gurule system, the sum of the number of 2 way crossings in 2 adjacent shell levels. (e.g. Q3 has 6 two way crossings, Q4 has 12, so 6 +12 = 18). Electron subshells appear to involve factors or subsets of those numbers.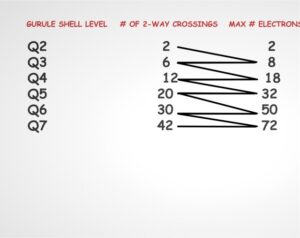

4. The circular waves constrain each other creating their own “boundary conditions” and hence a stable unit of matter. This fact invites us to reexamine the understanding of “forces” (strong, weak etc) and whether they are even necessary in this mode.

5. The Gurule System illustrates how waves weave together to form units of matter. Multiple DeBroglie matter waves in a 3d matrix. It also is consistent with aspects of debroglie-bohm pilot wave theory (https://www.quantamagazine.org/pilot-wave-theory-gains-experimental-support-20160516/)

6. The models may illustrate Gauge Symmetries . Worth investigating.

7. Shows the supersymmetry of super partners (particle pairs e.g. fermion/boson) and how the existence of one depends on the other
Looking at this field through the lens of General Semantics (Korsybski) one might surmise the existence of deeply fixed assumptions and perceptual biases underlying the way subatomic research is conducted by the mere fact the subatomic vernacular is overpopulated with nouns, as if they we were observing “things” not processes.

Ben Gurule spent his life searching for the truth that underlies physical reality. What he discovered may offer a unique view of some of the ongoing questions in physics. It will take time, consideration and peer reviewed research to determine if his work is of lasting significance. If that turns out to be the case, then such recognition will likely necessitate the formation of a new vocabulary to expand the lexicon of of subatomic study.